欧美在线日韩-欧美在线区-欧美在线看欧美视频免费网站-欧美在线精品一区二区在线观看-www..com黄-vr专区日韩精品中文字幕

作者 | Nikhil Garg，Navya Mehta 譯者 | 彎月 責編 | 蘇宓出品 | CSDN（ID：CSDNnews）

由于 AI 與機器學習的快速發展，如今向量數據庫已無處不在。雖然向量搜索能夠支持復雜的 AI 或機器學習應用程序，但這個概念本身并不難。在文本中，我們來一起看看向量數據庫的工作原理，并使用不到 200 行 Rust 代碼構建一個簡單的向量搜索庫。

GitHub 完整的代碼：https://github.com/fennel-ai/fann/?ref=fennel.ai

本文使用的方法基于流行庫 annoy 中使用的一種名叫“Locality Sensitive Hashing”（局部敏感哈希，LSH）的系列算法。本文的目的不是介紹一種新奇的算法或庫，而是分享如何編寫一個向量搜索。

在寫代碼之前，首先我們來介紹一下什么是向量搜索。

向量（又名嵌入）介紹

我們很難使用傳統的數據庫表示和查詢文檔、圖像、視頻等復雜的非結構化數據，尤其是無法查找“相似”數據。那么，YouTube 又是如何選擇下一個播放視頻的呢？Spotify 又是如何根據當前歌曲自定義播放列表的呢？

2010 年代 AI 的進步（從 Word2Vec 和 GloVe 開始）使我們能夠構建這些對象的語義表示，即使用笛卡爾空間中的點表示這些對象。假設一個視頻被映射到點 [0.1, -5.1, 7.55]，另一個被映射到點 [5.3, -0.1, 2.7]。這些機器學習算法的神奇之處在于，這些點的選擇保留了語義信息：兩個視頻的相似度越高，它們的向量之間的距離越小。

請注意，這些向量（或更專業的叫法是“嵌入”）不一定是三維的，它們可以、而且通常確實位于更高維的空間中（比如 128 維或 750 維）。而且距離也不一定是歐幾里得距離，其他形式的距離也可以，比如點積。無論采用哪種形式，重要的是它們之間的距離對應于相似性。

下面，假設我們可以訪問所有 YouTube 視頻的此類向量。那么我們如何找到與某個視頻相似度最高的其他視頻呢？很簡單。遍歷所有視頻，計算它們之間的距離，并選擇距離最小的視頻，這個過程又稱之為查找視頻的“最近鄰居”。這種方法確實有效，除了一個問題，線性O(N)搜索的成本過高。所以，我們需要一種更快的次線性方法來查找視頻的最近鄰居。這通常是不可能的，必須付出一些代價。

然而，在實際情況下，我們并不需要找到“最近”的視頻，只要足夠接近就可以了。這就是“近似最近鄰”（Approximate Nearest Neighbor，ANN）算法，又稱為向量搜索。我們的目標是通過次線性方法找到空間中任何足夠近的最近鄰。那么，實際如何實現呢？

如何找到近似最近鄰？

向量搜索算法背后的基本思想都是相同的：通過一些預處理來識別彼此足夠接近的點（有點類似于建立索引）。查詢時，使用這個“索引”來排除大部分點。只留下少量點，然后再進行線性掃描。

然而，這個簡單的想法有很多可以實現的方法。目前有幾種最先進的向量搜索算法，例如 HNSW（Hierarchical Navigable Small World，分層的可導航小世界）是一種圖，它連接了互相接近的頂點，而且還保存了距離固定入口點的長距離邊。此外還有一些開源項目，例如 Facebook 的 FAISS，以及一些高可用向量數據庫的 PaaS 產品，例如 Pinecone 和 Weaviate。

在本文中，假設有“N”個指定的點，我們要在這些點上構建一個簡化的向量搜索索引，步驟如下：

隨機抽取 2 個向量 A 和 B。

計算這兩個向量之間的中點 C。

構建一個通過 C 并垂直于連接 A 和 B 的線段的超平面（即更高維度的“線”）。

根據相對于超平面的位置：“上方”或“下方”，將所有向量分為兩組。

分別對兩組向量做以下處理：如果組的大小大于可配置參數“最大節點數”，則在該組之上遞歸調用此過程，構建子樹。否則，使用所有向量（或它們的唯一 ID）構建一個葉節點。

我們將使用這個隨機過程來構建一棵樹，其中的每個節點都是一個超平面定義，左邊的子樹是超平面“下方”的所有向量，右邊的子樹是超平面“上方”的所有向量。向量集不斷遞歸拆分，直到葉節點包含的向量不超過“最大節點數”。下圖是包含5個點的示例：

廣告

膽小者勿入！五四三二一...恐怖的躲貓貓游戲現在開始！

×

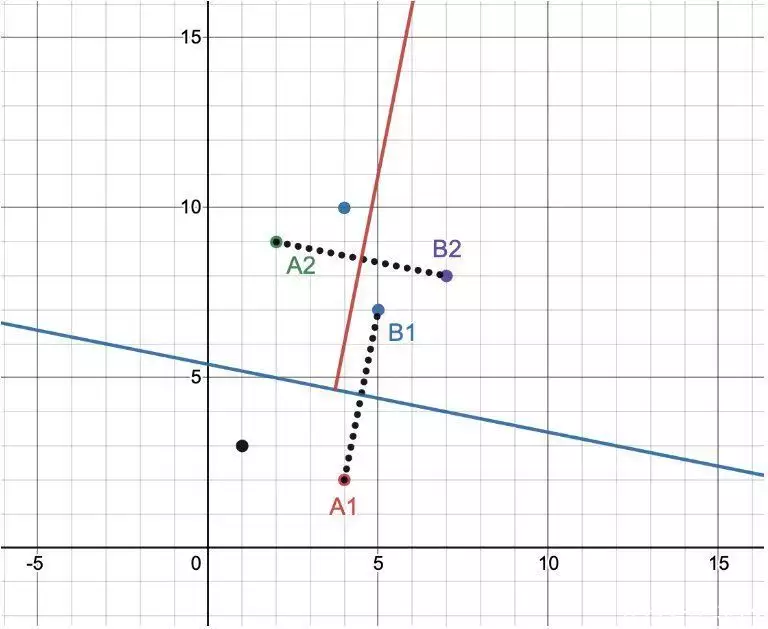
圖1：利用隨機超平面分割空間

我們隨機選擇向量 A1=(4,2)和 B1=(5,7)，二者的中點是 (4.5,4.5)，我們構建一條線，要求通過中點且垂直于線 (A1, B1)。這條線 x + 5y=27（圖中藍色的線）給了我們兩組向量：一組包含 2 個向量，另一組包含 4 個。假設“最大節點數”設置為 2。那么，**組向量不需要進一步拆分，而第二組向量需要進一步遞歸——如圖所示，我們又構建了一個紅色超平面。對于大型數據集，如此重復拆分可以將超空間拆分為幾個不同的區域，如下所示。

圖2：被許多超平面分割的空間（來自 https://t.co/K0Xlht8GwQ，作者：Erik Bernhardsson）

此處的每個區域代表一個葉節點，而且感覺足夠接近的點很可能最終會出現在同一個葉節點中。接下來，給定一個查詢點，我們可以在對數時間內自上而下遍歷樹，找到它所屬的葉子，然后對葉節點中的所有（數量不多）點進行線性掃描。很明顯，這個算法并不是萬無一失的，即便是距離非常近的兩個點也完全有可能被一個超平面分開，最終導致二者彼此相距很遠。但是，這個問題可以通過構建多棵獨立的樹來解決，這樣，如果兩個點之間的距離足夠近，它們出現在某些樹同一個葉節點中的概率就很高。在查詢時，我們自上而下遍歷所有樹，定位相關的葉節點，然后求所有葉節點的所有候選節點的并集，并對所有節點進行線性掃描。

好了，理論的介紹到此為止。下面，我們來編寫代碼。

首先，我們為 Rust 的 Vector 類型定義一些工具函數，包括求點積、均值、哈希值以及平方 L2 距離。感謝 Rust 的優雅的類型系統，我們可以傳遞泛型類型參數 N，以在編譯時強制索引中的所有向量具有相同的維度。

#[derive(Eq, PartialEq, Hash)]pub struct HashKey<const N: usize>([u32; N]);#[derive(Copy, Clone)]pub struct Vector<const N: usize>(pub [f32; N]);impl<const N: usize> Vector { pub fn subtract_from(&self, vector: &Vector) -> Vector { let mapped = self.0.iter().zip(vector.0).map(|(a, b)| b - a); let coords: [f32; N] = mapped.collect::>().try_into().unwrap(); return Vector(coords); } pub fn avg(&self, vector: &Vector) -> Vector { let mapped = self.0.iter().zip(vector.0).map(|(a, b)| (a + b) / 2.0); let coords: [f32; N] = mapped.collect::>().try_into().unwrap(); return Vector(coords); } pub fn dot_product(&self, vector: &Vector) -> f32 { let zipped_iter = self.0.iter().zip(vector.0); return zipped_iter.map(|(a, b)| a * b).sum::(); } pub fn to_hashkey(&self) -> HashKey { // f32 in Rust doesnt implement hash. We use bytes to dedup. While it // cant differentiate ~16M ways NaN is written, its safe for us let bit_iter = self.0.iter().map(|a| a.to_bits()); let data: [u32; N] = bit_iter.collect::>().try_into().unwrap(); return HashKey::(data); } pub fn sq_euc_dis(&self, vector: &Vector) -> f32 { let zipped_iter = self.0.iter().zip(vector.0); return zipped_iter.map(|(a, b)| (a - b).powi(2)).sum(); }}

構建好這些核心工具函數之后，下面我們來定義超平面：

struct HyperPlane<const N: usize> { coefficients: Vector, constant: f32,}impl<const N: usize> HyperPlane { pub fn point_is_above(&self, point: &Vector) -> bool { self.coefficients.dot_product(point) + self.constant >= 0.0 }}

接下來，我們來生成隨機超平面，構建最近鄰樹的森林。我們應該如何表示樹中的點呢？

我們可以直接將 D 維向量存儲在葉節點中。但是，如果這個維度（D）非常大，那么會導致內存碎片化（嚴重影響到性能），而且當多棵樹引用同一個向量時，還會造成森林重復保存。因此，我們將向量存儲在全局可訪問的連續位置中，并在葉節點中保存類型為 usize 的索引（在 64 位系統上僅占用 8 字節，相反如果直接保存四維向量，每個維度的 f32 類型就會占用 4 字節）。以下是用于表示樹內部節點和葉節點的數據類型。

enum Node<const N: usize> { Inner(Box<InnerNode<N>>), Leaf(Box<LeafNode<N>>),}struct LeafNode<const N: usize>(Vec<usize>);struct InnerNode<const N: usize> { hyperplane: HyperPlane<N>, left_node: Node<N>, right_node: Node<N>,}pub struct ANNIndex<const N: usize> { trees: Vec<Node<N>>, ids: Vec<i32>, values: Vec<Vector<N>>,}

那么，我們應該如何找到正確的超平面呢？

我們從索引中隨機采樣兩個，分別對應于向量 A 和 B，計算 n = A - B，并找到 A 和 B 的中點（point_on_plane）。存儲超平面使用的結構包含系數（向量 n）和常量（n 和 point_on_plane 的點積），形式為：n(x-x0) = nx - nx0。我們可以求向量和 n 之間的點積，然后減去常數，就可以將向量放在超平面的“上方”或“下方”。由于樹中的內部節點包含超平面定義，葉節點包含向量 ID，因此我們可以使用 ADT 對樹進行類型檢查：

impl ANNIndex { fn build_hyperplane( indexes: &Vec, all_vecs: &Vec>, ) -> (HyperPlane, Vec, Vec) { let sample: Vec = indexes .choose_multiple(&mut rand::thread_rng(), 2) .collect(); // cartesian eq for hyperplane n * (x - x_0) = 0 // n (normal vector) is the coefs x_1 to x_n let (a, b) = (*sample[0], *sample[1]); let coefficients = all_vecs[a].subtract_from(&all_vecs[b]); let point_on_plane = all_vecs[a].avg(&all_vecs[b]); let constant = -coefficients.dot_product(&point_on_plane); let hyperplane = HyperPlane:: { coefficients, constant, }; let (mut above, mut below) = (vec![], vec![]); for &id in indexes.iter() { if hyperplane.point_is_above(&all_vecs[id]) { above.push(id) } else { below.push(id) }; } return (hyperplane, above, below); }}

接下來，我們定義遞歸過程，根據索引時的“最大節點數”構建樹：

impl<const N: usize> ANNIndex { fn build_a_tree( max_size: i32, indexes: &Vec, all_vecs: &Vec>, ) -> Node { if indexes.len() as usize) { return Node::Leaf(Box::new(LeafNode::(indexes.clone()))); } let (plane, above, below) = Self::build_hyperplane(indexes, all_vecs); let node_above = Self::build_a_tree(max_size, &above, all_vecs); let node_below = Self::build_a_tree(max_size, &below, all_vecs); return Node::Inner(Box::new(InnerNode:: { hyperplane: plane, left_node: node_below, right_node: node_above, })); }}

請注意，由于該算法不允許重復，構建兩點之間的超平面要求這兩個點是唯一的，因此在建立索引之前，我們必須去除向量集中的重復項。

因此整個索引（樹的森林）可以這樣構建：

impl<const N: usize> ANNIndex { fn deduplicate( vectors: &Vec>, ids: &Vec, dedup_vectors: &mut Vec>, ids_of_dedup_vectors: &mut Vec, ) { let mut hashes_seen = HashSet::new(); for i in 1..vectors.len() { let hash_key = vectors[i].to_hashkey(); if !hashes_seen.contains(&hash_key) { hashes_seen.insert(hash_key); dedup_vectors.push(vectors[i]); ids_of_dedup_vectors.push(ids[i]); } } } pub fn build_index( num_trees: i32, max_size: i32, vecs: &Vec>, vec_ids: &Vec, ) -> ANNIndex { let (mut unique_vecs, mut ids) = (vec![], vec![]); Self::deduplicate(vecs, vec_ids, &mut unique_vecs, &mut ids); // Trees hold an index into the [unique_vecs] list which is not // necessarily its id, if duplicates existed let all_indexes: Vec = (0..unique_vecs.len()).collect(); let trees: Vec = (0..num_trees) .map(|_| Self::build_a_tree(max_size, &all_indexes, &unique_vecs)) .collect(); return ANNIndex::<N> { trees, ids, values: unique_vecs, }; }} 查詢時間

索引建立之后，下一步我們如何使用它搜索某棵樹中輸入向量的 K 個近似最近鄰？我們的超平面存儲在非葉節點處，因此我們可以從樹的根開始搜索：“這個向量是在這個超平面的上方還是下方？”我們可以用點積計算，復雜度為 O(D)。接下來，我們可以根據響應，遞歸搜索左子樹或右子樹，直到找到葉節點。請記住，葉節點中存儲的向量數最大為“最大節點數”，這些向量位于輸入向量的近似鄰域中（它們將落入所有超平面下超空間的同一分區中）。如果這個葉節點的向量索引數超過 K，我們就需要根據到輸入向量的 L2 距離，對所有這些向量進行排序，并返回最接近的 K 個向量。

假設我們的索引最后得到了一棵平衡樹，對于維度 D、向量數量 N 和最大節點數 M << N，搜索耗費的時間為 O(Dlog(N) + DM + Mlog(M))，最壞的情況下我們需要比較 log(N) 個超平面（即樹的高度）才能找到葉節點，每次比較耗費的時間為 O(D) 個點積，計算一個葉節點的所有候選向量的 L2 距離需要 O(DM)，最后在 O(Mlog(M)) 時間內對它們進行排序，并返回 前 K 個。

但是，如果我們找到的葉節點少于 K 個向量，會發生什么情況？如果最大節點數太小，或超平面分割不均勻，則會導致某個子樹中的向量非常少。為了解決這個問題，我們可以在樹搜索中添加一些簡單的回溯功能。例如，如果返回的候選向量數量不足，我們可以在內部節點再遞歸調用一次，訪問另一個分枝。代碼如下：

1impl<const N: usize> ANNIndex { 2 fn tree_result( 3 query: Vector, 4 n: i32, 5 tree: &Node, 6 candidates: &mut HashSet, 7 ) -> i32 { 8 // take everything in node, if still needed, take from alternate subtree 9 match tree {10 Node::Leaf(box_leaf) => {11 let leaf_values = &(box_leaf.0);12 let num_candidates_found = min(n as usize, leaf_values.len());13 for i in 0..num_candidates_found {14 candidates.insert(leaf_values[i]);15 }16 return num_candidates_found as i32;17 }18 Node::Inner(inner) => {19 let above = (*inner).hyperplane.point_is_above(&query);20 let (main, backup) = match above {21 true => (&(inner.right_node), &(inner.left_node)),22 false => (&(inner.left_node), &(inner.right_node)),23 };24 match Self::tree_result(query, n, main, candidates) {25 k if k < n => {26 k + Self::tree_result(query, n - k, backup, candidates)27 }28 k => k,29 }30 }31 }32 }33}

請注意，為了進一步優化遞歸調用，我們還可以保存子樹中的向量總數，并在每個內部節點中保存指向所有葉節點的指針列表，但為了簡單起見，此處略過。

將此搜索擴展到一片森林非常簡單，只需從所有樹木中單獨收集前 K 個候選者，按距離對它們進行排序，然后返回總體的前 K 個匹配項。請注意，隨著樹的數量增加，內存的使用和搜索時間都會呈線性增長，但我們可以獲得更好的“更近”鄰居，因為我們收集了來自不同樹的候選者。

1impl<const N: usize> ANNIndex { 2 pub fn search_approximate( 3 &self, 4 query: Vector, 5 top_k: i32, 6 ) -> Vec { 7 let mut candidates = HashSet::new(); 8 for tree in self.trees.iter() { 9 Self::tree_result(query, top_k, tree, &mut candidates);10 }11 candidates12 .into_iter()13 .map(|idx| (idx, self.values[idx].sq_euc_dis(&query)))14 .sorted_by(|a, b| a.1.partial_cmp(&b.1).unwrap())15 .take(top_k as usize)16 .map(|(idx, dis)| (self.ids[idx], dis))17 .collect()18 }19}

以上就是一個簡單的向量搜索索引的 200 行 Rust 代碼！

基準測試

其實，這個實現非常簡單，以至于我們一度懷疑相較于最先進的算法，這個算法非常拙略。因此，我們做了一些基準測試來證實我們的懷疑。

算法可以通過延遲和質量來評估。質量通常通過召回率來衡量：求近似最近鄰搜索返回結果與線性搜索返回結果的百分比。嚴格來說，有時返回的結果并不在前 K，但非常接近 K，因此也沒關系，為了量化這一點，我們可以計算鄰居的平均歐幾里德距離，并將其與平均距離進行比較。

測量延遲很簡單，我們可以檢查執行查詢所需的時間。

所有的基準測試都是在搭載了 2.3 GHz 四核英特爾酷睿 i5 處理器的機器上運行的，使用了 999,994 條維基百科數據 FastText 嵌入，300 個維度。我們設置返回“前 K 個”查詢結果。

作為參考，我們拿 FAISS HNSW 索引（ef_search=16、ef_construction=40、max_node_size=15）與 Rust 索引的小型版本（num_trees=3、max_node_size=15）進行了比較。我們使用 Rust 實現了窮舉搜索，而 FAISS 庫有 HNSW 的 C++ 源代碼。原始延遲數突出了近似搜索的優勢：

兩種近似最近鄰方法快了三個數量級。看起來在這個微型基準測試中，我們的 Rust 實現比 HNSW 快 3 倍。

在分析質量時，我們的測試數據為：返回“river”的 10 個最近的鄰居。

再來一個例子，這次我們搜索“war”。

我們使用的這個語料庫包含 999,994 個單詞，我們可視化了在 HNSW 和我們的自定義 Rust 索引下，每個單詞與其前 K=20 個近似鄰居的平均歐幾里得距離的分布：

廣告

從秘書起步，十年內無人超越，以一己之力力挽狂瀾成就一段傳奇

×

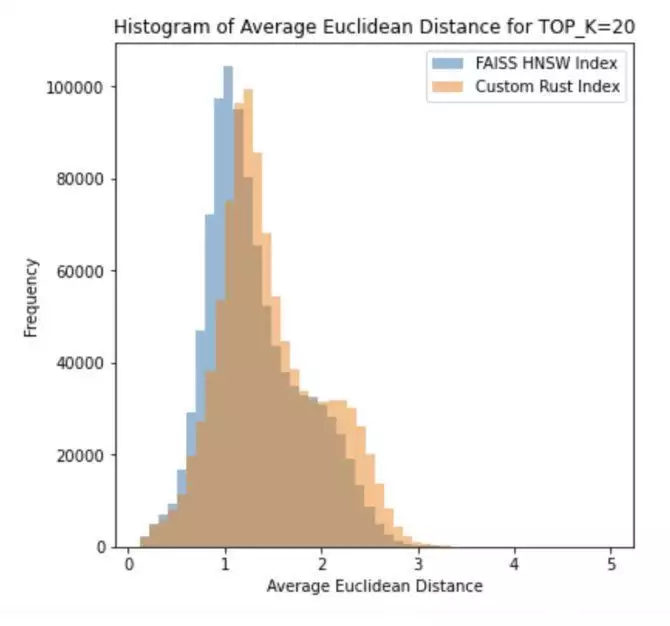
最先進的 HNSW 索引提供的鄰居確實比我們的示例索引更近，其平均距離和中值距離分別為 1.31576 和 1.20230（而與我們的示例索引分別為 1.47138 和 1.35620）。在大小為 1 萬的子集上，HNSW 的前 K=20 的召回率為 58.2%，而我們的示例索引在不同配置下的測試結果如下：

為什么我們的算法如此之快？

通過上面的數字可以看出，雖然我們的算法在質量上無法與尖端技術相媲美，但它的速度非常快。為什么會這樣？

老實說，在構建這個算法時，我們興奮得昏了頭腦，性能優化也只是為了好玩。下面是一些重要的優化：

將去除文檔的重復數據的過程轉移到索引冷路徑上。通過索引（而不是浮點數組）引用向量可以大幅提高搜索速度，因為跨樹查找唯一候選者只需要對 8 字節索引進行散列（而不是 300 維 f32 數據）。

在將點添加到全局候選列表之前，散列并查找唯一向量，通過遞歸搜索調用中的可變引用傳遞數據，以避免棧幀之間和棧幀內的復制。

將 N 作為通用類型參數傳遞進去，這樣類型檢查就會將 300 維的數據當作長度為 300 的 f32 數組，這不僅可以改善緩存局部性，還可以減少內存占用。

我們懷疑內部操作（例如點積）被 Rust 編譯器向量化了，但我們沒有檢查。

一些真實世界應用的考慮

有一些問題這個示例沒有考慮到，但在生產環境的向量搜索中非常關鍵：

當搜索涉及多個樹時應當使用并行。不要順序收集候選者，而是應該并行進行，因為每個樹都會訪問完全不同的內存，因此每個樹都可以在各自的線程上單獨運行，候選者通過通道發送到主線程。線程可以在創建索引時建立，并使用模擬搜索進行預熱（將樹加載到緩存），從而減小搜索的額外開銷。這樣搜索就不會根據樹的數量線性增長了。

大型樹可能無法完整地加載到內存中，可能需要從磁盤中讀取，所以可以將特定的子圖放到磁盤上，并精心設計算法，保證搜索正常工作的同時，盡可能減小文件I/O。

繼續深入，如果樹無法保存在一個實例的磁盤上，可以將子樹分布到多個實例中，并讓遞歸搜索在本地數據不存在時發出RPC請求。

樹包含許多內存重定向（基于指針的樹對L1緩存不友好）。平衡樹可以寫成數組，但我們的樹只是接近平衡，其超平面是隨機的。是否可能采用新的數據結構？

上述問題的解決方案，對于新數據即時編制索引也是成立的（可能需要對大型樹進行分片）。如果特定索引序列會導致非常不平衡的樹，那么是否應該重建樹？

這些都是我們未來該深刻思考的問題。

原文鏈接：https://fennel.ai/blog/vector-search-in-200-lines-of-rust/

聲明：本文為 CSDN 翻譯，未經允許，禁止轉載。