
【CSDN 編者按】相比一個人一種風格的代碼,幾乎人人都想編寫一套“整潔”的代碼,然而,遵循條條框框規則寫出來的代碼,在性能上能否可以達到理想狀態?
來自 Molly Rocket 公司的首席程序員 Casey Muratori 給出了否定的答案,與此同時,他也以教科書中的示例進行了測試,最終得出“遵循編寫整潔代碼的這些規則,你的代碼運行速度會放慢 15 倍”的結論。
不過,對于這樣的結論也引發了巨大的爭議,代碼的性能和整潔度能否共存?接下來,我們將通過本文一探究竟。
原文鏈接:https://www.computerenhance.com/p/clean-code-horrible-performance
聲明:本文為 CSDN 翻譯,未經允許,禁止轉載
作者 | Casey Muratori譯者 | 彎月 責編 | 蘇宓出品 | CSDN(ID:CSDNnews)編寫“整潔”的代碼,這是一條反復被人提及的編程建議,尤其是初學者,聽得太多耳朵都長繭了。“整潔”的代碼背后是一長串規則,告訴你應該怎么書寫,代碼才能保持“整潔”。
實際上,這些規則中很大的一部分并不會影響代碼的運行時間。我們無法客觀評估這些類型的規則,而且也沒必要進行這樣的評估。然而,一些所謂的“整潔”代碼規則(其中有一部分甚至被反復強調)是可以客觀衡量的,因為它們確實會影響代碼的運行時行為。
整理和歸納“整潔”的代碼規則,并提取實際影響代碼結構的規則,我們將得到:
使用多態代替“if/else”和“switch”;
代碼不應該知道使用對象的內部結構;
嚴格控制函數的規模;
函數應該只做一件事;
“DRY”(Don’t Repeat Yourself):不要重復自己。
這些規則非常具體地說明了為了保持代碼“整潔”,我們應該如何書寫特定的代碼片段。然而,我的疑問在于,如果創建一段遵循這些規則的代碼,它的性能如何?
為了構建我認為嚴格遵守“整潔之道”的代碼,我使用了“整潔”代碼相關文章中包含的現有示例。也就是說,這些代碼不是我編寫的,我只是利用他們提供的示例代碼來評估“整潔”代碼倡導的規則。
那些年我們見過的“整潔”代碼
提起“整潔”代碼的示例,你經常會看到下面這樣的代碼:
/* ======================================================================== LISTING 22 ======================================================================== */class shape_base{public: shape_base() {} virtual f32 Area() = 0;};class square : public shape_base{public: square(f32 SideInit) : Side(SideInit) {} virtual f32 Area() {return Side*Side;}private: f32 Side;};class rectangle : public shape_base{public: rectangle(f32 WidthInit, f32 HeightInit) : Width(WidthInit), Height(HeightInit) {} virtual f32 Area() {return Width*Height;}private: f32 Width, Height;};class triangle : public shape_base{public: triangle(f32 BaseInit, f32 HeightInit) : Base(BaseInit), Height(HeightInit) {} virtual f32 Area() {return 0.5f*Base*Height;}private: f32 Base, Height;};class circle : public shape_base{public: circle(f32 RadiusInit) : Radius(RadiusInit) {} virtual f32 Area() {return Pi32*Radius*Radius;}private: f32 Radius;};這段代碼是一個形狀的基類,從中派生出了一些特定的形狀:圓形、三角形、矩形、正方形。此外,還有一個計算面積的虛函數。
就像規則要求的一樣,我們傾向于多態性,函數只做一件事,而且很小。最終,我們得到了一個“整潔”的類層次結構,每個派生類都知道如何計算自己的面積,并存儲了計算面積所需的數據。
如果我們想象使用這個層次結構來做某事,比如計算一系列形狀的總面積,那么我們希望看到下面這樣的代碼:
/* ======================================================================== LISTING 23 ======================================================================== */f32 TotalAreaVTBL(u32 ShapeCount, shape_base **Shapes){ f32 Accum = 0.0f; for(u32 ShapeIndex = 0; ShapeIndex { Accum += Shapes[ShapeIndex]->Area(); } return Accum;}你可能會發現,此處我沒有使用任何迭代,因為“整潔代碼之道”中沒有建議你必須使用迭代器。因此,我想盡可能避免有損“整潔”代碼的寫法,我不希望添加任何有可能混淆編譯器并導致性能下降的抽象迭代器。
此外,你可能還會注意到,這個循環是在一個指針數組上進行的。這是使用類層次結構的直接結果:我們不知道每種形狀占用的內存有多大。所以除非我們添加另一個虛函數調用來獲取每個形狀的數據大小,并使用某種步長可變的跳躍過程來遍歷它們,否則我們需要指針來找出每個形狀的實際開始位置。
因為這個計算數一個累加和,所以循環本身引起的依賴可能會導致循環速度減慢。由于計算累加可以以任意順序進行,為了安全起見,我還寫了一個手動展開的版本:
/* ======================================================================== LISTING 24 ======================================================================== */f32 TotalAreaVTBL4(u32 ShapeCount, shape_base **Shapes){ f32 Accum0 = 0.0f; f32 Accum1 = 0.0f; f32 Accum2 = 0.0f; f32 Accum3 = 0.0f; u32 Count = ShapeCount/4; while(Count--) { Accum0 += Shapes[0]->Area(); Accum1 += Shapes[1]->Area(); Accum2 += Shapes[2]->Area(); Accum3 += Shapes[3]->Area(); Shapes += 4; } f32 Result = (Accum0 + Accum1 + Accum2 + Accum3); return Result;}在一個簡單的測試工具中運行以上這兩個例程,可以粗略地計算出執行該操作每個形狀所需的循環總數:
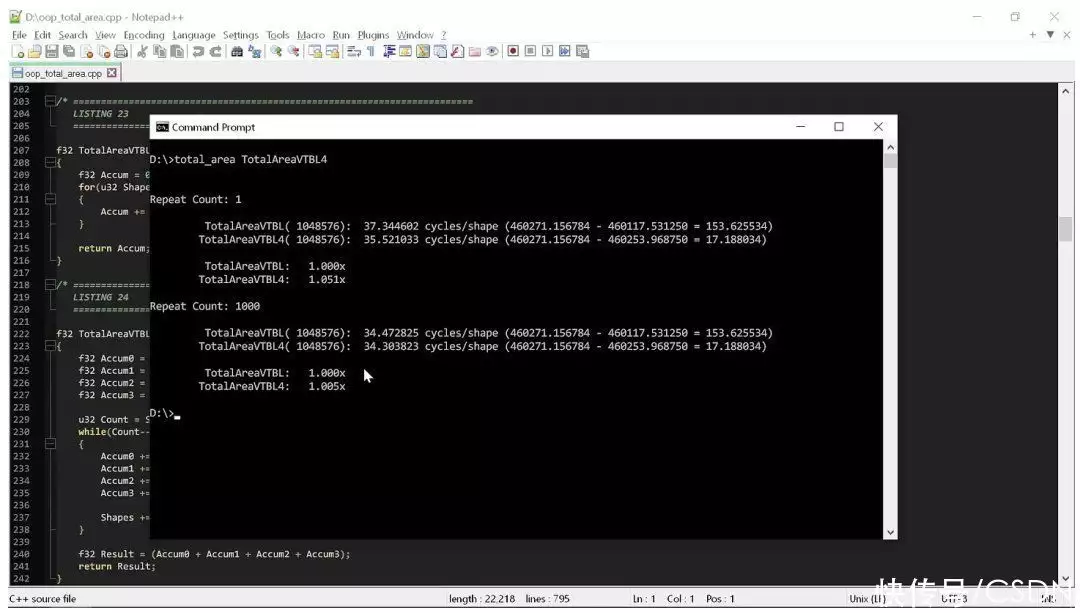
測試工具以兩種不同的方式統計代碼的時間。**種方法是只運行一次代碼,以顯示在沒有預熱的狀態下代碼的運行時間(在此狀態下,數據應該在 L3 中,但 L2 和 L1 已被刷新,而且分支預測器尚未針對循環進行預測)。
第二種方法是反復運行代碼,看看當緩存和分支預測器以最適合循環的方式運行時情況會怎樣。請注意,這些都不是嚴謹的測量,因為正如你所見,我們已經看到了巨大的差異,根本不需要任何嚴謹的分析工具。
從結果中我們可以看出,這兩個例程之間沒有太大區別。這段“整潔”的代碼計算這個形狀的面積大約需要循環35次,如果幸運的話,有可能減少到34次。
所以,我們嚴格遵守“代碼整潔之道”,最后需要循環35次。
違反“代碼整潔之道”的**條規則后
那么,如果我們違反**條規則,會怎么樣?如果我們不使用多態性,使用一個 switch 語句呢?
下面,我又編寫了一段一模一樣的代碼,只不過這一次我沒有使用類層次結構,而是使用枚舉,將所有內容扁平化為一個結構的形狀類型:
/* ======================================================================== LISTING 25 ======================================================================== */enum shape_type : u32{ Shape_Square, Shape_Rectangle, Shape_Triangle, Shape_Circle, Shape_Count,};struct shape_union{ shape_type Type; f32 Width; f32 Height;};f32 GetAreaSwitch(shape_union Shape){ f32 Result = 0.0f; switch(Shape.Type) { case Shape_Square: {Result = Shape.Width*Shape.Width;} break; case Shape_Rectangle: {Result = Shape.Width*Shape.Height;} break; case Shape_Triangle: {Result = 0.5f*Shape.Width*Shape.Height;} break; case Shape_Circle: {Result = Pi32*Shape.Width*Shape.Width;} break; case Shape_Count: {} break; } return Result;}這是代碼整潔之道出現以前,很常見的“老派”寫法。
請注意,由于我們沒有為每個形狀提供特定的數據類型,所以如果某個類型缺乏其中一個值(比如“高度”),計算就不使用了。
現在,這個結構的用戶獲取面積不再需要調用虛函數,而是需要使用帶有 switch 語句的函數,這違反了“代碼整潔之道”。即便如此,你會注意到代碼更加簡潔了,但功能基本相同。switch 語句的每一個 case 的都對應于類層次結構中的一個虛函數。
對于求和循環本身,你可以看到這段代碼與上述“整潔”版幾乎相同:
/* ======================================================================== LISTING 26 ======================================================================== */f32 TotalAreaSwitch(u32 ShapeCount, shape_union *Shapes){ f32 Accum = 0.0f; for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex) { Accum += GetAreaSwitch(Shapes[ShapeIndex]); } return Accum;}f32 TotalAreaSwitch4(u32 ShapeCount, shape_union *Shapes){ f32 Accum0 = 0.0f; f32 Accum1 = 0.0f; f32 Accum2 = 0.0f; f32 Accum3 = 0.0f; ShapeCount /= 4; while(ShapeCount--) { Accum0 += GetAreaSwitch(Shapes[0]); Accum1 += GetAreaSwitch(Shapes[1]); Accum2 += GetAreaSwitch(Shapes[2]); Accum3 += GetAreaSwitch(Shapes[3]); Shapes += 4; } f32 Result = (Accum0 + Accum1 + Accum2 + Accum3); return Result;}唯一的不同之處在于,我們調用常規函數來獲取面積。
但是,我們已經看到了相較于類層次結構,使用扁平結構的直接好處:形狀可以存儲在數組中,不需要指針。不需要間接訪問,因為所有形狀占用的內存大小都一樣。
另外,我們還獲得了額外的好處,現在編譯器可以確切地看到我們在這個循環中做了什么,因為它只需查看 GetAreaSwitch 函數。它不必假設只有等到運行時我們才能看得見某些虛擬面積函數具體在做什么。
那么,編譯器能利用這些好處為我們做什么呢?下面,我們來完整地運行一遍四個形狀的面積計算,得到的結果如下:
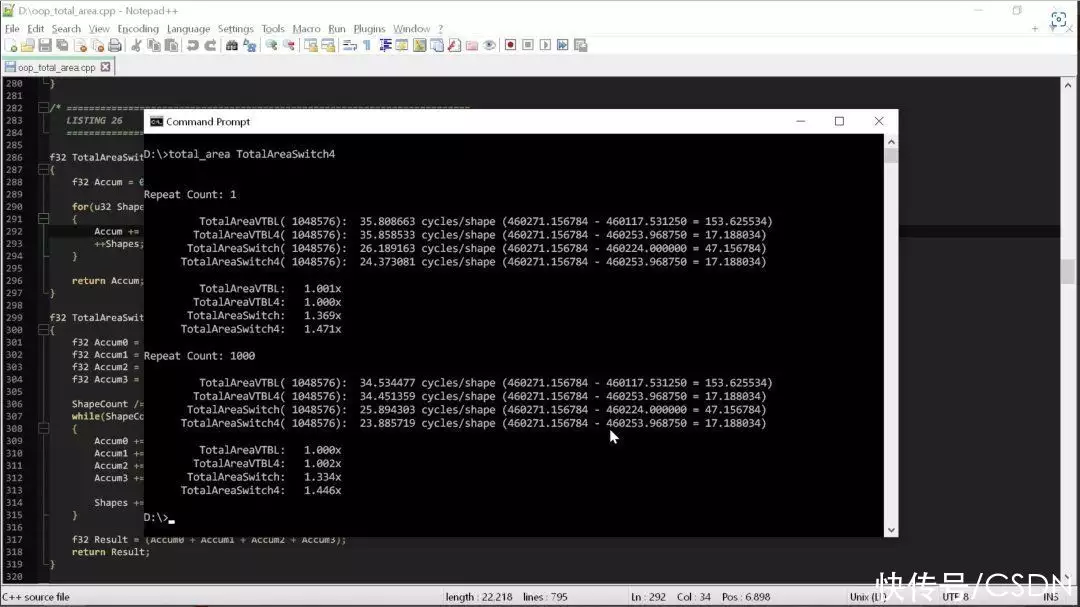
觀察結果,我們可以看出,改用“老派””的寫法后,代碼的性能立即提高了 1.5 倍。我們什么都沒干,只是刪除了使用 C++ 多態性的代碼,就收獲了1.5倍的性能提升。
違反代碼整潔之道的**條規則(也是核心原則之一),計算每個面積的循環數量就從35次減少到了24次,這意味著,遵循代碼整潔之道會導致代碼的速度降低1.5倍。拿手機打個比方,就相當于把 iPhone 14 Pro Max 換成了 iPhone 11 Pro Max。過去三四年間硬件的發展瞬間化無,僅僅是因為有人說要使用多態性,不要使用 switch 語句。
然而,這只是一個開頭。
違反“代碼整潔之道”的更多條規則后
如果我們違反更多規則,結果會怎么樣?如果我們打破第二條規則,“沒有內部知識”,結果會如何?如果我們的函數可以利用自身實際操作的知識來提高效率呢?
回顧一下計算面積的 switch 語句,你會發現所有面積的計算方式都很相似:
case Shape_Square: {Result = Shape.Width*Shape.Width;} break; case Shape_Rectangle: {Result = Shape.Width*Shape.Height;} break; case Shape_Triangle: {Result = 0.5f*Shape.Width*Shape.Height;} break; case Shape_Circle: {Result = Pi32*Shape.Width*Shape.Width;} break;所有形狀的面積計算都是做乘法,長乘以寬、寬乘以高,或者乘以 π 的系數等等。只不過,三角形的面積需要乘以1/2,而圓的面積需要乘以 π。
這是我認為此處使用 switch 語句非常合適的原因之一,盡管這與代碼整潔之道背道而馳。透過 switch 語句,我們可以很清楚地看到這種模式。當你按照操作而不是類型組織代碼時,觀察和提取通用模式就很簡單。相比之下,觀察類版本,你可能永遠也發現不了這種模式,因為類版本不僅有很多樣板代碼,而且你需要將每個類放在一個單獨的文件中,無法并排比較。
所以,從架構的角度來看,我一般都不贊成類層次結構,但這不是重點。我想說的是,我們可以通過上述發現的模式大大簡化 switch 語句。
請記住:這不是我選擇的示例,這可是整潔代碼倡導者用于說明的示例。所以,我并沒有刻意選擇一個恰巧能夠抽出一個模式的例子,因此這種現象應該比較普遍,因為大多數相似類型都有類似的算法結構,就像這個例子一樣。
為了利用這種模式,首先我們可以引入一個簡單的表,說明每種類型的面積計算需要使用哪個系數。其次,對于圓和正方形之類只需要一個參數(圓的參數為半徑,正方形的參數為邊長)的形狀,我們可以認為它們的長和寬恰巧相同,這樣我們就可以創建一個非常簡單的計算面積的函數:
/* ======================================================================== LISTING 27 ======================================================================== */f32 const CTable[Shape_Count] = {1.0f, 1.0f, 0.5f, Pi32};f32 GetAreaUnion(shape_union Shape){ f32 Result = CTable[Shape.Type]*Shape.Width*Shape.Height; return Result;}這個版本的兩個求和循環完全相同,無需修改,我們只需要將 GetAreaSwitch 換成 GetAreaUnion,其他代碼保持不變。
下面,我們來看看使用這個新版本的效果:

我們可以看到,從基于類型的思維模式切換到基于函數的思維模式,我們獲得了巨大的速度提升。從 switch 語句(相較于整潔代碼版本性能已經提升了 1.5 倍)換成表驅動的版本,速度全面提升了 10 倍。
我們只是添加了一個表查找和一行代碼,僅此而已!現在不僅代碼的運行速度大幅提升,而且語義的復雜性也顯著降低。標記更少、操作更少、代碼更少。
將數據模型與所需的操作融合到一起后,計算每個面積的循環數量減少到了 3.0~3.5 次。與遵循代碼整潔之道前兩條規則的代碼相比,這個版本的速度提高了 10 倍。
10 倍的性能提升非常巨大,我甚至無法拿 iPhone 做類比,即便是 iPhone 6(現代基準測試中最古老的手機)也只比最新的iPhone 14 Pro Max 慢 3 倍左右。
如果是線程桌面性能,10 倍的速度提升就相當于如今的 CPU 退回到2010年。代碼整潔之道的前兩條規則抹殺了 12 年的硬件發展。
然而,這個測試只是一個非常簡單的操作。我們還沒有探討“函數應該只做一件事”以及“盡可能保持小”。如果我們調整一下問題,全面遵循這些規則,結果會怎么樣?
下面這段代碼的層次結構完全相同,但這次我添加了一個虛函數,用于獲取每個形狀的角的個數:
/* ======================================================================== LISTING 32 ======================================================================== */class shape_base{public: shape_base() {} virtual f32 Area() = 0; virtual u32 CornerCount() = 0;};class square : public shape_base{public: square(f32 SideInit) : Side(SideInit) {} virtual f32 Area() {return Side*Side;} virtual u32 CornerCount() {return 4;}private: f32 Side;};class rectangle : public shape_base{public: rectangle(f32 WidthInit, f32 HeightInit) : Width(WidthInit), Height(HeightInit) {} virtual f32 Area() {return Width*Height;} virtual u32 CornerCount() {return 4;}private: f32 Width, Height;};class triangle : public shape_base{public: triangle(f32 BaseInit, f32 HeightInit) : Base(BaseInit), Height(HeightInit) {} virtual f32 Area() {return 0.5f*Base*Height;} virtual u32 CornerCount() {return 3;}private: f32 Base, Height;};class circle : public shape_base{public: circle(f32 RadiusInit) : Radius(RadiusInit) {} virtual f32 Area() {return Pi32*Radius*Radius;} virtual u32 CornerCount() {return 0;}private: f32 Radius;};長方形有4個角,三角形有3個,圓為0。接下來,我們來修改問題的定義,原來的問題是計算一系列形狀的面積之和,我們改為計算角加權的面積總和:總面積之和乘以角的數量。當然,這只是一個例子,實際工作中不會遇到。
下面,我們來更新“整潔”的求和循環,我們需要添加必要的數學運算,還需要多調用一次虛函數:
f32 CornerAreaVTBL(u32 ShapeCount, shape_base **Shapes){ f32 Accum = 0.0f; for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex) { Accum += (1.0f / (1.0f + (f32)Shapes[ShapeIndex]->CornerCount())) * Shapes[ShapeIndex]->Area(); } return Accum;}f32 CornerAreaVTBL4(u32 ShapeCount, shape_base **Shapes){ f32 Accum0 = 0.0f; f32 Accum1 = 0.0f; f32 Accum2 = 0.0f; f32 Accum3 = 0.0f; u32 Count = ShapeCount/4; while(Count--) { Accum0 += (1.0f / (1.0f + (f32)Shapes[0]->CornerCount())) * Shapes[0]->Area(); Accum1 += (1.0f / (1.0f + (f32)Shapes[1]->CornerCount())) * Shapes[1]->Area(); Accum2 += (1.0f / (1.0f + (f32)Shapes[2]->CornerCount())) * Shapes[2]->Area(); Accum3 += (1.0f / (1.0f + (f32)Shapes[3]->CornerCount())) * Shapes[3]->Area(); Shapes += 4; } f32 Result = (Accum0 + Accum1 + Accum2 + Accum3); return Result;}其實,我應該單獨寫一個函數,添加另一層間接。為了保證對“整潔”代碼采取疑罪從無的原則,我明確保留了這些代碼。
switch 語句的版本也需要相同的修改。首先,我們再添加一個 switch 語句來處理角的數量,case 語句與層次結構版本完全相同:
/* ======================================================================== LISTING 34 ======================================================================== */u32 GetCornerCountSwitch(shape_type Type){ u32 Result = 0; switch(Type) { case Shape_Square: {Result = 4;} break; case Shape_Rectangle: {Result = 4;} break; case Shape_Triangle: {Result = 3;} break; case Shape_Circle: {Result = 0;} break; case Shape_Count: {} break; } return Result;}接下來,我們按照相同的方式計算面積:
/* ======================================================================== LISTING 35 ======================================================================== */f32 CornerAreaSwitch(u32 ShapeCount, shape_union *Shapes){ f32 Accum = 0.0f; for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex) { Accum += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[ShapeIndex].Type))) * GetAreaSwitch(Shapes[ShapeIndex]); } return Accum;}f32 CornerAreaSwitch4(u32 ShapeCount, shape_union *Shapes){ f32 Accum0 = 0.0f; f32 Accum1 = 0.0f; f32 Accum2 = 0.0f; f32 Accum3 = 0.0f; ShapeCount /= 4; while(ShapeCount--) { Accum0 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[0].Type))) * GetAreaSwitch(Shapes[0]); Accum1 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[1].Type))) * GetAreaSwitch(Shapes[1]); Accum2 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[2].Type))) * GetAreaSwitch(Shapes[2]); Accum3 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[3].Type))) * GetAreaSwitch(Shapes[3]); Shapes += 4; } f32 Result = (Accum0 + Accum1 + Accum2 + Accum3); return Result;}與直接求面積總和的版本相同,類層次結構與 switch 語句的實現代碼幾乎相同。唯一的區別是,調用虛函數還是使用 switch 語句。
下面再來看看表驅動的寫法,你可以看到將操作和數據融合在一起的效果有多棒。與所有其他版本不同,在這個版本中,唯一需要修改的只有表中的值。我們并不需要獲取形狀的次要信息,我們可以將角的個數和面積系數直接放入表中,而代碼保持不變:
/* ======================================================================== LISTING 36 ======================================================================== */f32 const CTable[Shape_Count] = {1.0f / (1.0f + 4.0f), 1.0f / (1.0f + 4.0f), 0.5f / (1.0f + 3.0f), Pi32};f32 GetCornerAreaUnion(shape_union Shape){ f32 Result = CTable[Shape.Type]*Shape.Width*Shape.Height; return Result;}運行上述所有“角加權面積”函數,我們可以看到它們的性能受第二個形狀屬性的影響程度:

如你所見,“整潔”代碼的性能更糟糕。在直接計算面積時,switch 語句版本的速度快了 1.5 倍,而如今快了將近2倍,而查找表版本快了近 15 倍。
這說明“整潔”的代碼存在更深層次的問題:問題越復雜,代碼整潔之道對性能的損害就越大。當你嘗試將代碼整潔之道擴展到具有許多屬性的對象時,代碼的性能普遍會遭受損失。
使用代碼整潔之道的次數越多,編譯器就越不清楚你在干什么。一切都在單獨的翻譯單元中,在虛函數調用的后面。無論編譯器多么聰明,都無法優化這種代碼。
更糟糕的是,你無法使用此類代碼處理復雜的邏輯。如上所述,如果你的代碼庫圍繞函數而建,那么一些簡單的功能(例如將值提取到表中和刪除 switch 語句)很容易實現。但是,如果圍繞類型而建,那么實際就會困難得多,若非大量重寫,甚至可能無法實現。
我們只是添加了一個屬性,速度差異就從 10 倍增至 15 倍。這就像 2023 年的硬件退步到了 2008 年。
然而,也許你已經注意到了,我甚至沒有提到優化。除了保證不產生循環帶來的依賴之外,出于測試的目的,我沒有做任何優化!
如果我使用一個略微優化過的 AVX 版本運行這些例程,得到的結果如下:

速度差異在 20~25 倍之間,當然,沒有任何 AVX 優化的代碼使用了類似于代碼整潔之道的原則。
以上,我們只提到了4個原則,還有第五個呢?
老實說,“不要重復自己”似乎很好。如上所述,我們沒有重復自己。也許你會說,四個計算累加和的展開版本有重復的嫌疑,但這只是為了演示目的。實際上,我們不必同時保留這兩個例程。
如果“不要重復自己”有更嚴格的要求,比如不要構建兩個不同的表來編碼相同系數的版本,那么我就有不同意見了,因為有時我們必須這樣做才能獲得合理的性能。但是,一般來說,“不要重復自己”只是意味著不要重復編寫完全相同的代碼,所以聽起來像是一個合理的建議。
最重要的是,我們不必違反它來編寫能夠獲得合理性能的代碼。
“遵循整潔代碼的規則,你的代碼運行速度會降低15倍。”
因此,對于整潔代碼之道實際影響代碼結構的五條建議,我可能只會考慮一條,其余四條就算了。因為正如你所見,遵循這些建議會嚴重影響軟件的性能。
有人認為,遵循代碼整潔之道編寫的代碼更易于維護。然而,即便這是真的,我們也不得不考慮:“代價是什么?”
我們不可能只是為了減輕程序員的負擔,而放棄性能,導致硬件性能后退十年或更長時間。我們的工作是編寫在給定的硬件上運行良好的程序。如果這些規則會導致軟件的性能變差,那就是不可接受的。
最后,我們應該嘗試提出經驗法則,幫助保持代碼井井有條、易于維護和易于閱讀。這些目標本身沒什么問題,然而因此提出的這些規則有待思考。下次,再談論這些規則時,我希望加上一條備注:“遵循這些規則,你的代碼運行速度會變得慢15倍。”
“整潔”的代碼和性能可否兼得?
事實上,理想與現實往往存在一定的差距,如工整的字跡一樣,人人都希望能看到整潔代碼,但并非人人都能夠做到,然而不做不到不意味規則有問題。對此,一些網友也開啟了熱議模式:
網友 1:
我認為作者將通用建議應用到了一個特殊情況。
違反了整潔代碼之道的**條規則(也是核心原則之一),計算每個面積的循環數量就從35次減少到了24次。
大多數現代軟件的99.9%時間都花在等待用戶輸入上,僅花費0.1%的時間實際計算。如果你正在編寫3A游戲或高性能計算軟件,那么當然可以瘋狂優化,獲得這些改進。
但我們大多數人都不是這樣做的。大多數開發人員只不過是添加計劃中的下一個功能。整潔的代碼可以讓功能更快問世,而不是為了讓 CPU 做更少的工作。
網友 2:一個經常被引用的經驗法則:先跑起來,再讓它變得好看,再提高速度——要按照這個順序。也就是說,如果你的代碼一開始就很整潔,性能瓶頸就更容易找到和解決。
我有時希望我的項目中有性能問題,但實際上,性能問題經常出現在更高的層次,或者架構的層面上。比如一個API網關在一個循環中針對SAP服務器發出了太多的查詢。這會執行數十億行代碼,但性能的根源是為什么操作員會一次性點擊許多個鏈接。
除了學校作業,我從來沒有遇到過性能問題。但我遇到過很多情況,我不得不處理寫得不好(“不整潔”)的代碼,并耗費大量腦細胞來理解這些代碼。
為此,你是否覺得”整潔的代碼“與性能是相互沖突的呢?
