【CSDN 編者按】相比一個人一種風(fēng)格的代碼，幾乎人人都想編寫一套“整潔”的代碼，然而，遵循條條框框規(guī)則寫出來的代碼，在性能上能否可以達(dá)到理想狀態(tài)？
來自 Molly Rocket 公司的首席程序員 Casey Muratori 給出了否定的答案，與此同時，他也以教科書中的示例進(jìn)行了測試，最終得出“遵循編寫整潔代碼的這些規(guī)則，你的代碼運(yùn)行速度會放慢 15 倍”的結(jié)論。
不過，對于這樣的結(jié)論也引發(fā)了巨大的爭議，代碼的性能和整潔度能否共存？接下來，我們將通過本文一探究竟。
原文鏈接：https://www.computerenhance.com/p/clean-code-horrible-performance
聲明：本文為 CSDN 翻譯，未經(jīng)允許，禁止轉(zhuǎn)載
作者 | Casey Muratori譯者 | 彎月 責(zé)編 | 蘇宓出品 | CSDN（ID：CSDNnews）編寫“整潔”的代碼，這是一條反復(fù)被人提及的編程建議，尤其是初學(xué)者，聽得太多耳朵都長繭了。“整潔”的代碼背后是一長串規(guī)則，告訴你應(yīng)該怎么書寫，代碼才能保持“整潔”。
實(shí)際上，這些規(guī)則中很大的一部分并不會影響代碼的運(yùn)行時間。我們無法客觀評估這些類型的規(guī)則，而且也沒必要進(jìn)行這樣的評估。然而，一些所謂的“整潔”代碼規(guī)則（其中有一部分甚至被反復(fù)強(qiáng)調(diào)）是可以客觀衡量的，因?yàn)樗鼈兇_實(shí)會影響代碼的運(yùn)行時行為。
整理和歸納“整潔”的代碼規(guī)則，并提取實(shí)際影響代碼結(jié)構(gòu)的規(guī)則，我們將得到：
使用多態(tài)代替“if/else”和“switch”；
代碼不應(yīng)該知道使用對象的內(nèi)部結(jié)構(gòu)；
嚴(yán)格控制函數(shù)的規(guī)模；
函數(shù)應(yīng)該只做一件事；
“DRY”（Don’t Repeat Yourself）：不要重復(fù)自己。
這些規(guī)則非常具體地說明了為了保持代碼“整潔”，我們應(yīng)該如何書寫特定的代碼片段。然而，我的疑問在于，如果創(chuàng)建一段遵循這些規(guī)則的代碼，它的性能如何？
為了構(gòu)建我認(rèn)為嚴(yán)格遵守“整潔之道”的代碼，我使用了“整潔”代碼相關(guān)文章中包含的現(xiàn)有示例。也就是說，這些代碼不是我編寫的，我只是利用他們提供的示例代碼來評估“整潔”代碼倡導(dǎo)的規(guī)則。
那些年我們見過的“整潔”代碼
提起“整潔”代碼的示例，你經(jīng)常會看到下面這樣的代碼：
/* ======================================================================== LISTING 22 ======================================================================== */class shape_base{public: shape_base() {} virtual f32 Area() = 0;};class square : public shape_base{public: square(f32 SideInit) : Side(SideInit) {} virtual f32 Area() {return Side*Side;}private: f32 Side;};class rectangle : public shape_base{public: rectangle(f32 WidthInit, f32 HeightInit) : Width(WidthInit), Height(HeightInit) {} virtual f32 Area() {return Width*Height;}private: f32 Width, Height;};class triangle : public shape_base{public: triangle(f32 BaseInit, f32 HeightInit) : Base(BaseInit), Height(HeightInit) {} virtual f32 Area() {return 0.5f*Base*Height;}private: f32 Base, Height;};class circle : public shape_base{public: circle(f32 RadiusInit) : Radius(RadiusInit) {} virtual f32 Area() {return Pi32*Radius*Radius;}private: f32 Radius;};這段代碼是一個形狀的基類，從中派生出了一些特定的形狀：圓形、三角形、矩形、正方形。此外，還有一個計(jì)算面積的虛函數(shù)。
就像規(guī)則要求的一樣，我們傾向于多態(tài)性，函數(shù)只做一件事，而且很小。最終，我們得到了一個“整潔”的類層次結(jié)構(gòu)，每個派生類都知道如何計(jì)算自己的面積，并存儲了計(jì)算面積所需的數(shù)據(jù)。
如果我們想象使用這個層次結(jié)構(gòu)來做某事，比如計(jì)算一系列形狀的總面積，那么我們希望看到下面這樣的代碼：
/* ======================================================================== LISTING 23 ======================================================================== */f32 TotalAreaVTBL(u32 ShapeCount, shape_base **Shapes){ f32 Accum = 0.0f; for(u32 ShapeIndex = 0; ShapeIndex { Accum += Shapes[ShapeIndex]->Area(); } return Accum;}你可能會發(fā)現(xiàn)，此處我沒有使用任何迭代，因?yàn)椤罢麧嵈a之道”中沒有建議你必須使用迭代器。因此，我想盡可能避免有損“整潔”代碼的寫法，我不希望添加任何有可能混淆編譯器并導(dǎo)致性能下降的抽象迭代器。
此外，你可能還會注意到，這個循環(huán)是在一個指針數(shù)組上進(jìn)行的。這是使用類層次結(jié)構(gòu)的直接結(jié)果：我們不知道每種形狀占用的內(nèi)存有多大。所以除非我們添加另一個虛函數(shù)調(diào)用來獲取每個形狀的數(shù)據(jù)大小，并使用某種步長可變的跳躍過程來遍歷它們，否則我們需要指針來找出每個形狀的實(shí)際開始位置。
因?yàn)檫@個計(jì)算數(shù)一個累加和，所以循環(huán)本身引起的依賴可能會導(dǎo)致循環(huán)速度減慢。由于計(jì)算累加可以以任意順序進(jìn)行，為了安全起見，我還寫了一個手動展開的版本：
/* ======================================================================== LISTING 24 ======================================================================== */f32 TotalAreaVTBL4(u32 ShapeCount, shape_base **Shapes){ f32 Accum0 = 0.0f; f32 Accum1 = 0.0f; f32 Accum2 = 0.0f; f32 Accum3 = 0.0f; u32 Count = ShapeCount/4; while(Count--) { Accum0 += Shapes[0]->Area(); Accum1 += Shapes[1]->Area(); Accum2 += Shapes[2]->Area(); Accum3 += Shapes[3]->Area(); Shapes += 4; } f32 Result = (Accum0 + Accum1 + Accum2 + Accum3); return Result;}在一個簡單的測試工具中運(yùn)行以上這兩個例程，可以粗略地計(jì)算出執(zhí)行該操作每個形狀所需的循環(huán)總數(shù)：
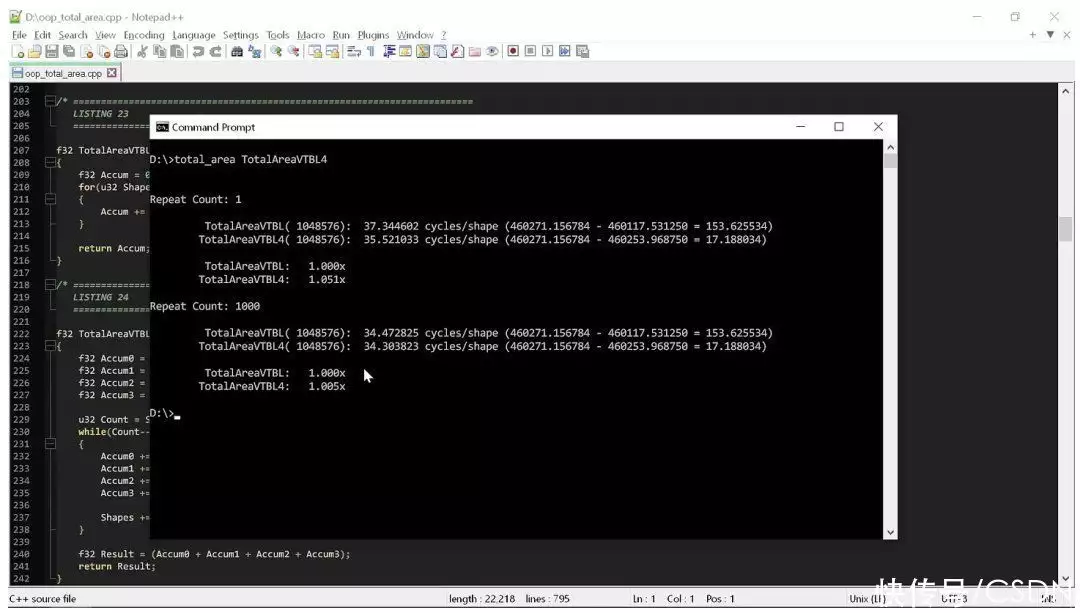
測試工具以兩種不同的方式統(tǒng)計(jì)代碼的時間。**種方法是只運(yùn)行一次代碼，以顯示在沒有預(yù)熱的狀態(tài)下代碼的運(yùn)行時間（在此狀態(tài)下，數(shù)據(jù)應(yīng)該在 L3 中，但 L2 和 L1 已被刷新，而且分支預(yù)測器尚未針對循環(huán)進(jìn)行預(yù)測）。
第二種方法是反復(fù)運(yùn)行代碼，看看當(dāng)緩存和分支預(yù)測器以最適合循環(huán)的方式運(yùn)行時情況會怎樣。請注意，這些都不是嚴(yán)謹(jǐn)?shù)臏y量，因?yàn)檎缒闼姡覀円呀?jīng)看到了巨大的差異，根本不需要任何嚴(yán)謹(jǐn)?shù)姆治龉ぞ摺?/span>
從結(jié)果中我們可以看出，這兩個例程之間沒有太大區(qū)別。這段“整潔”的代碼計(jì)算這個形狀的面積大約需要循環(huán)35次，如果幸運(yùn)的話，有可能減少到34次。
所以，我們嚴(yán)格遵守“代碼整潔之道”，最后需要循環(huán)35次。
違反“代碼整潔之道”的**條規(guī)則后
那么，如果我們違反**條規(guī)則，會怎么樣？如果我們不使用多態(tài)性，使用一個 switch 語句呢？
下面，我又編寫了一段一模一樣的代碼，只不過這一次我沒有使用類層次結(jié)構(gòu)，而是使用枚舉，將所有內(nèi)容扁平化為一個結(jié)構(gòu)的形狀類型：
/* ======================================================================== LISTING 25 ======================================================================== */enum shape_type : u32{ Shape_Square, Shape_Rectangle, Shape_Triangle, Shape_Circle, Shape_Count,};struct shape_union{ shape_type Type; f32 Width; f32 Height;};f32 GetAreaSwitch(shape_union Shape){ f32 Result = 0.0f; switch(Shape.Type) { case Shape_Square: {Result = Shape.Width*Shape.Width;} break; case Shape_Rectangle: {Result = Shape.Width*Shape.Height;} break; case Shape_Triangle: {Result = 0.5f*Shape.Width*Shape.Height;} break; case Shape_Circle: {Result = Pi32*Shape.Width*Shape.Width;} break; case Shape_Count: {} break; } return Result;}這是代碼整潔之道出現(xiàn)以前，很常見的“老派”寫法。
請注意，由于我們沒有為每個形狀提供特定的數(shù)據(jù)類型，所以如果某個類型缺乏其中一個值（比如“高度”），計(jì)算就不使用了。
現(xiàn)在，這個結(jié)構(gòu)的用戶獲取面積不再需要調(diào)用虛函數(shù)，而是需要使用帶有 switch 語句的函數(shù)，這違反了“代碼整潔之道”。即便如此，你會注意到代碼更加簡潔了，但功能基本相同。switch 語句的每一個 case 的都對應(yīng)于類層次結(jié)構(gòu)中的一個虛函數(shù)。
對于求和循環(huán)本身，你可以看到這段代碼與上述“整潔”版幾乎相同：
/* ======================================================================== LISTING 26 ======================================================================== */f32 TotalAreaSwitch(u32 ShapeCount, shape_union *Shapes){ f32 Accum = 0.0f; for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex) { Accum += GetAreaSwitch(Shapes[ShapeIndex]); } return Accum;}f32 TotalAreaSwitch4(u32 ShapeCount, shape_union *Shapes){ f32 Accum0 = 0.0f; f32 Accum1 = 0.0f; f32 Accum2 = 0.0f; f32 Accum3 = 0.0f; ShapeCount /= 4; while(ShapeCount--) { Accum0 += GetAreaSwitch(Shapes[0]); Accum1 += GetAreaSwitch(Shapes[1]); Accum2 += GetAreaSwitch(Shapes[2]); Accum3 += GetAreaSwitch(Shapes[3]); Shapes += 4; } f32 Result = (Accum0 + Accum1 + Accum2 + Accum3); return Result;}唯一的不同之處在于，我們調(diào)用常規(guī)函數(shù)來獲取面積。
但是，我們已經(jīng)看到了相較于類層次結(jié)構(gòu)，使用扁平結(jié)構(gòu)的直接好處：形狀可以存儲在數(shù)組中，不需要指針。不需要間接訪問，因?yàn)樗行螤钫加玫膬?nèi)存大小都一樣。
另外，我們還獲得了額外的好處，現(xiàn)在編譯器可以確切地看到我們在這個循環(huán)中做了什么，因?yàn)樗恍璨榭?GetAreaSwitch 函數(shù)。它不必假設(shè)只有等到運(yùn)行時我們才能看得見某些虛擬面積函數(shù)具體在做什么。
那么，編譯器能利用這些好處為我們做什么呢？下面，我們來完整地運(yùn)行一遍四個形狀的面積計(jì)算，得到的結(jié)果如下：
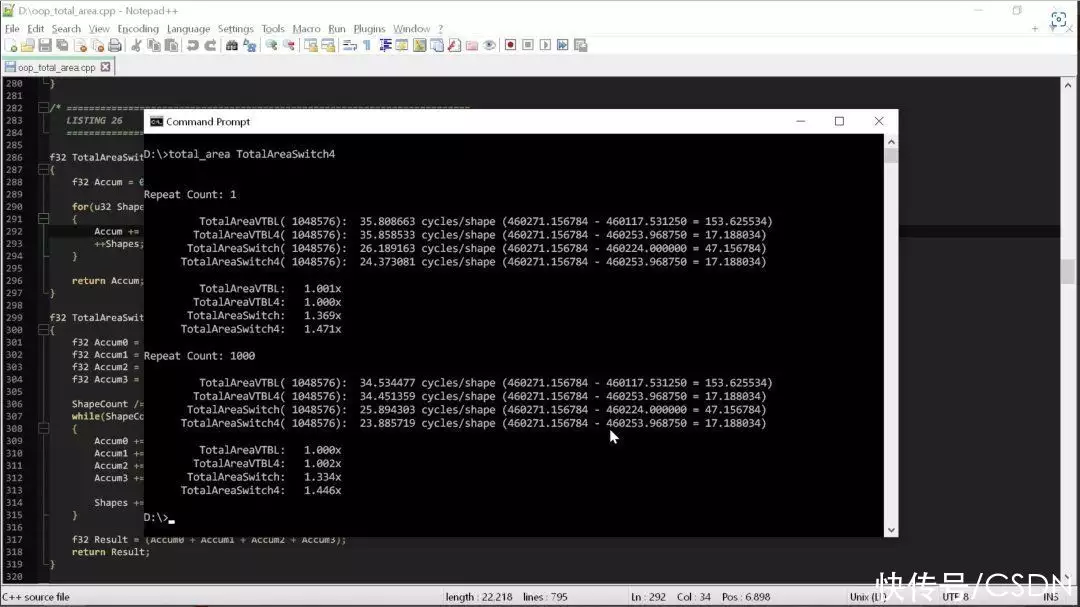
觀察結(jié)果，我們可以看出，改用“老派””的寫法后，代碼的性能立即提高了 1.5 倍。我們什么都沒干，只是刪除了使用 C++ 多態(tài)性的代碼，就收獲了1.5倍的性能提升。
違反代碼整潔之道的**條規(guī)則（也是核心原則之一），計(jì)算每個面積的循環(huán)數(shù)量就從35次減少到了24次，這意味著，遵循代碼整潔之道會導(dǎo)致代碼的速度降低1.5倍。拿手機(jī)打個比方，就相當(dāng)于把 iPhone 14 Pro Max 換成了 iPhone 11 Pro Max。過去三四年間硬件的發(fā)展瞬間化無，僅僅是因?yàn)橛腥苏f要使用多態(tài)性，不要使用 switch 語句。
然而，這只是一個開頭。
違反“代碼整潔之道”的更多條規(guī)則后
如果我們違反更多規(guī)則，結(jié)果會怎么樣？如果我們打破第二條規(guī)則，“沒有內(nèi)部知識”，結(jié)果會如何？如果我們的函數(shù)可以利用自身實(shí)際操作的知識來提高效率呢？
回顧一下計(jì)算面積的 switch 語句，你會發(fā)現(xiàn)所有面積的計(jì)算方式都很相似：
case Shape_Square: {Result = Shape.Width*Shape.Width;} break; case Shape_Rectangle: {Result = Shape.Width*Shape.Height;} break; case Shape_Triangle: {Result = 0.5f*Shape.Width*Shape.Height;} break; case Shape_Circle: {Result = Pi32*Shape.Width*Shape.Width;} break;所有形狀的面積計(jì)算都是做乘法，長乘以寬、寬乘以高，或者乘以 π 的系數(shù)等等。只不過，三角形的面積需要乘以1/2，而圓的面積需要乘以 π。
這是我認(rèn)為此處使用 switch 語句非常合適的原因之一，盡管這與代碼整潔之道背道而馳。透過 switch 語句，我們可以很清楚地看到這種模式。當(dāng)你按照操作而不是類型組織代碼時，觀察和提取通用模式就很簡單。相比之下，觀察類版本，你可能永遠(yuǎn)也發(fā)現(xiàn)不了這種模式，因?yàn)轭惏姹静粌H有很多樣板代碼，而且你需要將每個類放在一個單獨(dú)的文件中，無法并排比較。
所以，從架構(gòu)的角度來看，我一般都不贊成類層次結(jié)構(gòu)，但這不是重點(diǎn)。我想說的是，我們可以通過上述發(fā)現(xiàn)的模式大大簡化 switch 語句。
請記住：這不是我選擇的示例，這可是整潔代碼倡導(dǎo)者用于說明的示例。所以，我并沒有刻意選擇一個恰巧能夠抽出一個模式的例子，因此這種現(xiàn)象應(yīng)該比較普遍，因?yàn)榇蠖鄶?shù)相似類型都有類似的算法結(jié)構(gòu)，就像這個例子一樣。
為了利用這種模式，首先我們可以引入一個簡單的表，說明每種類型的面積計(jì)算需要使用哪個系數(shù)。其次，對于圓和正方形之類只需要一個參數(shù)（圓的參數(shù)為半徑，正方形的參數(shù)為邊長）的形狀，我們可以認(rèn)為它們的長和寬恰巧相同，這樣我們就可以創(chuàng)建一個非常簡單的計(jì)算面積的函數(shù)：
/* ======================================================================== LISTING 27 ======================================================================== */f32 const CTable[Shape_Count] = {1.0f, 1.0f, 0.5f, Pi32};f32 GetAreaUnion(shape_union Shape){ f32 Result = CTable[Shape.Type]*Shape.Width*Shape.Height; return Result;}這個版本的兩個求和循環(huán)完全相同，無需修改，我們只需要將 GetAreaSwitch 換成 GetAreaUnion，其他代碼保持不變。
下面，我們來看看使用這個新版本的效果：
我們可以看到，從基于類型的思維模式切換到基于函數(shù)的思維模式，我們獲得了巨大的速度提升。從 switch 語句（相較于整潔代碼版本性能已經(jīng)提升了 1.5 倍）換成表驅(qū)動的版本，速度全面提升了 10 倍。
我們只是添加了一個表查找和一行代碼，僅此而已！現(xiàn)在不僅代碼的運(yùn)行速度大幅提升，而且語義的復(fù)雜性也顯著降低。標(biāo)記更少、操作更少、代碼更少。
將數(shù)據(jù)模型與所需的操作融合到一起后，計(jì)算每個面積的循環(huán)數(shù)量減少到了 3.0～3.5 次。與遵循代碼整潔之道前兩條規(guī)則的代碼相比，這個版本的速度提高了 10 倍。
10 倍的性能提升非常巨大，我甚至無法拿 iPhone 做類比，即便是 iPhone 6（現(xiàn)代基準(zhǔn)測試中最古老的手機(jī)）也只比最新的iPhone 14 Pro Max 慢 3 倍左右。
如果是線程桌面性能，10 倍的速度提升就相當(dāng)于如今的 CPU 退回到2010年。代碼整潔之道的前兩條規(guī)則抹殺了 12 年的硬件發(fā)展。
然而，這個測試只是一個非常簡單的操作。我們還沒有探討“函數(shù)應(yīng)該只做一件事”以及“盡可能保持小”。如果我們調(diào)整一下問題，全面遵循這些規(guī)則，結(jié)果會怎么樣？
下面這段代碼的層次結(jié)構(gòu)完全相同，但這次我添加了一個虛函數(shù)，用于獲取每個形狀的角的個數(shù)：
/* ======================================================================== LISTING 32 ======================================================================== */class shape_base{public: shape_base() {} virtual f32 Area() = 0; virtual u32 CornerCount() = 0;};class square : public shape_base{public: square(f32 SideInit) : Side(SideInit) {} virtual f32 Area() {return Side*Side;} virtual u32 CornerCount() {return 4;}private: f32 Side;};class rectangle : public shape_base{public: rectangle(f32 WidthInit, f32 HeightInit) : Width(WidthInit), Height(HeightInit) {} virtual f32 Area() {return Width*Height;} virtual u32 CornerCount() {return 4;}private: f32 Width, Height;};class triangle : public shape_base{public: triangle(f32 BaseInit, f32 HeightInit) : Base(BaseInit), Height(HeightInit) {} virtual f32 Area() {return 0.5f*Base*Height;} virtual u32 CornerCount() {return 3;}private: f32 Base, Height;};class circle : public shape_base{public: circle(f32 RadiusInit) : Radius(RadiusInit) {} virtual f32 Area() {return Pi32*Radius*Radius;} virtual u32 CornerCount() {return 0;}private: f32 Radius;};長方形有4個角，三角形有3個，圓為0。接下來，我們來修改問題的定義，原來的問題是計(jì)算一系列形狀的面積之和，我們改為計(jì)算角加權(quán)的面積總和：總面積之和乘以角的數(shù)量。當(dāng)然，這只是一個例子，實(shí)際工作中不會遇到。
下面，我們來更新“整潔”的求和循環(huán)，我們需要添加必要的數(shù)學(xué)運(yùn)算，還需要多調(diào)用一次虛函數(shù)：
f32 CornerAreaVTBL(u32 ShapeCount, shape_base **Shapes){ f32 Accum = 0.0f; for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex) { Accum += (1.0f / (1.0f + (f32)Shapes[ShapeIndex]->CornerCount())) * Shapes[ShapeIndex]->Area(); } return Accum;}f32 CornerAreaVTBL4(u32 ShapeCount, shape_base **Shapes){ f32 Accum0 = 0.0f; f32 Accum1 = 0.0f; f32 Accum2 = 0.0f; f32 Accum3 = 0.0f; u32 Count = ShapeCount/4; while(Count--) { Accum0 += (1.0f / (1.0f + (f32)Shapes[0]->CornerCount())) * Shapes[0]->Area(); Accum1 += (1.0f / (1.0f + (f32)Shapes[1]->CornerCount())) * Shapes[1]->Area(); Accum2 += (1.0f / (1.0f + (f32)Shapes[2]->CornerCount())) * Shapes[2]->Area(); Accum3 += (1.0f / (1.0f + (f32)Shapes[3]->CornerCount())) * Shapes[3]->Area(); Shapes += 4; } f32 Result = (Accum0 + Accum1 + Accum2 + Accum3); return Result;}其實(shí)，我應(yīng)該單獨(dú)寫一個函數(shù)，添加另一層間接。為了保證對“整潔”代碼采取疑罪從無的原則，我明確保留了這些代碼。
switch 語句的版本也需要相同的修改。首先，我們再添加一個 switch 語句來處理角的數(shù)量，case 語句與層次結(jié)構(gòu)版本完全相同：
/* ======================================================================== LISTING 34 ======================================================================== */u32 GetCornerCountSwitch(shape_type Type){ u32 Result = 0; switch(Type) { case Shape_Square: {Result = 4;} break; case Shape_Rectangle: {Result = 4;} break; case Shape_Triangle: {Result = 3;} break; case Shape_Circle: {Result = 0;} break; case Shape_Count: {} break; } return Result;}接下來，我們按照相同的方式計(jì)算面積：
/* ======================================================================== LISTING 35 ======================================================================== */f32 CornerAreaSwitch(u32 ShapeCount, shape_union *Shapes){ f32 Accum = 0.0f; for(u32 ShapeIndex = 0; ShapeIndex < ShapeCount; ++ShapeIndex) { Accum += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[ShapeIndex].Type))) * GetAreaSwitch(Shapes[ShapeIndex]); } return Accum;}f32 CornerAreaSwitch4(u32 ShapeCount, shape_union *Shapes){ f32 Accum0 = 0.0f; f32 Accum1 = 0.0f; f32 Accum2 = 0.0f; f32 Accum3 = 0.0f; ShapeCount /= 4; while(ShapeCount--) { Accum0 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[0].Type))) * GetAreaSwitch(Shapes[0]); Accum1 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[1].Type))) * GetAreaSwitch(Shapes[1]); Accum2 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[2].Type))) * GetAreaSwitch(Shapes[2]); Accum3 += (1.0f / (1.0f + (f32)GetCornerCountSwitch(Shapes[3].Type))) * GetAreaSwitch(Shapes[3]); Shapes += 4; } f32 Result = (Accum0 + Accum1 + Accum2 + Accum3); return Result;}與直接求面積總和的版本相同，類層次結(jié)構(gòu)與 switch 語句的實(shí)現(xiàn)代碼幾乎相同。唯一的區(qū)別是，調(diào)用虛函數(shù)還是使用 switch 語句。
下面再來看看表驅(qū)動的寫法，你可以看到將操作和數(shù)據(jù)融合在一起的效果有多棒。與所有其他版本不同，在這個版本中，唯一需要修改的只有表中的值。我們并不需要獲取形狀的次要信息，我們可以將角的個數(shù)和面積系數(shù)直接放入表中，而代碼保持不變：
/* ======================================================================== LISTING 36 ======================================================================== */f32 const CTable[Shape_Count] = {1.0f / (1.0f + 4.0f), 1.0f / (1.0f + 4.0f), 0.5f / (1.0f + 3.0f), Pi32};f32 GetCornerAreaUnion(shape_union Shape){ f32 Result = CTable[Shape.Type]*Shape.Width*Shape.Height; return Result;}運(yùn)行上述所有“角加權(quán)面積”函數(shù)，我們可以看到它們的性能受第二個形狀屬性的影響程度：
如你所見，“整潔”代碼的性能更糟糕。在直接計(jì)算面積時，switch 語句版本的速度快了 1.5 倍，而如今快了將近2倍，而查找表版本快了近 15 倍。
這說明“整潔”的代碼存在更深層次的問題：問題越復(fù)雜，代碼整潔之道對性能的損害就越大。當(dāng)你嘗試將代碼整潔之道擴(kuò)展到具有許多屬性的對象時，代碼的性能普遍會遭受損失。
使用代碼整潔之道的次數(shù)越多，編譯器就越不清楚你在干什么。一切都在單獨(dú)的翻譯單元中，在虛函數(shù)調(diào)用的后面。無論編譯器多么聰明，都無法優(yōu)化這種代碼。
更糟糕的是，你無法使用此類代碼處理復(fù)雜的邏輯。如上所述，如果你的代碼庫圍繞函數(shù)而建，那么一些簡單的功能（例如將值提取到表中和刪除 switch 語句）很容易實(shí)現(xiàn)。但是，如果圍繞類型而建，那么實(shí)際就會困難得多，若非大量重寫，甚至可能無法實(shí)現(xiàn)。
我們只是添加了一個屬性，速度差異就從 10 倍增至 15 倍。這就像 2023 年的硬件退步到了 2008 年。
然而，也許你已經(jīng)注意到了，我甚至沒有提到優(yōu)化。除了保證不產(chǎn)生循環(huán)帶來的依賴之外，出于測試的目的，我沒有做任何優(yōu)化！
如果我使用一個略微優(yōu)化過的 AVX 版本運(yùn)行這些例程，得到的結(jié)果如下：
速度差異在 20～25 倍之間，當(dāng)然，沒有任何 AVX 優(yōu)化的代碼使用了類似于代碼整潔之道的原則。
以上，我們只提到了4個原則，還有第五個呢？
老實(shí)說，“不要重復(fù)自己”似乎很好。如上所述，我們沒有重復(fù)自己。也許你會說，四個計(jì)算累加和的展開版本有重復(fù)的嫌疑，但這只是為了演示目的。實(shí)際上，我們不必同時保留這兩個例程。
如果“不要重復(fù)自己”有更嚴(yán)格的要求，比如不要構(gòu)建兩個不同的表來編碼相同系數(shù)的版本，那么我就有不同意見了，因?yàn)橛袝r我們必須這樣做才能獲得合理的性能。但是，一般來說，“不要重復(fù)自己”只是意味著不要重復(fù)編寫完全相同的代碼，所以聽起來像是一個合理的建議。
最重要的是，我們不必違反它來編寫能夠獲得合理性能的代碼。
“遵循整潔代碼的規(guī)則，你的代碼運(yùn)行速度會降低15倍。”
因此，對于整潔代碼之道實(shí)際影響代碼結(jié)構(gòu)的五條建議，我可能只會考慮一條，其余四條就算了。因?yàn)檎缒闼姡裱@些建議會嚴(yán)重影響軟件的性能。
有人認(rèn)為，遵循代碼整潔之道編寫的代碼更易于維護(hù)。然而，即便這是真的，我們也不得不考慮：“代價是什么？”
我們不可能只是為了減輕程序員的負(fù)擔(dān)，而放棄性能，導(dǎo)致硬件性能后退十年或更長時間。我們的工作是編寫在給定的硬件上運(yùn)行良好的程序。如果這些規(guī)則會導(dǎo)致軟件的性能變差，那就是不可接受的。
最后，我們應(yīng)該嘗試提出經(jīng)驗(yàn)法則，幫助保持代碼井井有條、易于維護(hù)和易于閱讀。這些目標(biāo)本身沒什么問題，然而因此提出的這些規(guī)則有待思考。下次，再談?wù)撨@些規(guī)則時，我希望加上一條備注：“遵循這些規(guī)則，你的代碼運(yùn)行速度會變得慢15倍。”
“整潔”的代碼和性能可否兼得？
事實(shí)上，理想與現(xiàn)實(shí)往往存在一定的差距，如工整的字跡一樣，人人都希望能看到整潔代碼，但并非人人都能夠做到，然而不做不到不意味規(guī)則有問題。對此，一些網(wǎng)友也開啟了熱議模式：
網(wǎng)友 1：
我認(rèn)為作者將通用建議應(yīng)用到了一個特殊情況。
違反了整潔代碼之道的**條規(guī)則（也是核心原則之一），計(jì)算每個面積的循環(huán)數(shù)量就從35次減少到了24次。
大多數(shù)現(xiàn)代軟件的99.9％時間都花在等待用戶輸入上，僅花費(fèi)0.1％的時間實(shí)際計(jì)算。如果你正在編寫3A游戲或高性能計(jì)算軟件，那么當(dāng)然可以瘋狂優(yōu)化，獲得這些改進(jìn)。
但我們大多數(shù)人都不是這樣做的。大多數(shù)開發(fā)人員只不過是添加計(jì)劃中的下一個功能。整潔的代碼可以讓功能更快問世，而不是為了讓 CPU 做更少的工作。
網(wǎng)友 2：一個經(jīng)常被引用的經(jīng)驗(yàn)法則：先跑起來，再讓它變得好看，再提高速度——要按照這個順序。也就是說，如果你的代碼一開始就很整潔，性能瓶頸就更容易找到和解決。
我有時希望我的項(xiàng)目中有性能問題，但實(shí)際上，性能問題經(jīng)常出現(xiàn)在更高的層次，或者架構(gòu)的層面上。比如一個API網(wǎng)關(guān)在一個循環(huán)中針對SAP服務(wù)器發(fā)出了太多的查詢。這會執(zhí)行數(shù)十億行代碼，但性能的根源是為什么操作員會一次性點(diǎn)擊許多個鏈接。
除了學(xué)校作業(yè)，我從來沒有遇到過性能問題。但我遇到過很多情況，我不得不處理寫得不好（“不整潔”）的代碼，并耗費(fèi)大量腦細(xì)胞來理解這些代碼。
為此，你是否覺得”整潔的代碼“與性能是相互沖突的呢？
